Статистический смысл волновой функции

По просьбе нашего читателя постараемся описанную тему от 20:21 | 11.02.2017 раскрыть ещё глубже, сегодня рассмотрим Статистический смысл волновой функции. Не будем разливать воду, а преступим рассмотрению этого вопроса.

Основное положение

Главной задачей классической механики выступает определение положения макрообъекта в какой-то из моментов времени. С этой целью составляется система уравнений, при решении которой определяется зависимость радиус-вектора от времени. В классической механике состояние частицы в момент ее движения в каждый определенный момент задается двумя величинами радиус-вектором и импульсом.

Таким образом, классическое описание движения частицы оказывается правомерным, если осуществляется в области с характерным размером, намного большим длины волны де Бройля. В противном случае (вблизи ядра атома, например) принимаются во внимание волновые свойства микрочастиц. На ограниченную применимость классического описания микрообъектов с волновыми свойствами указывают и соотношения неопределенностей.

Теория, направленная на описание движения малых частиц (при учете их волновых свойств), будет называться квантовой (волновой) механикой.

Рисунок 2. Волновая функция микрочастиц.

Волновая функция представляет комплексную функцию, описывая состояние частицы в каждой из точек пространства и для любого момента времени. Понимание физического смысла волновой функции дают опыты с дифракцией электронов. Вследствие них, четкие дифракционные картины будут обнаруживаться даже в случае направления на мишень одиночных электронов (когда каждый последующий электрон начинает испускаться после достижения предыдущим экрана).

После такой довольно длительной по времени «бомбардировки» картина на экране в точности будет соответствовать получаемой при одновременном направлении на мишень множества электронов картине. Это приводит к выводу о подчинении движения любой микрочастицы по отдельности вероятностным (статистическим) закономерностям. Также становится очевидным, что в момент направления на мишень одиночного электрона, точка на экране (в которой будет его фиксация) заранее не может быть предсказана со стопроцентной уверенностью.

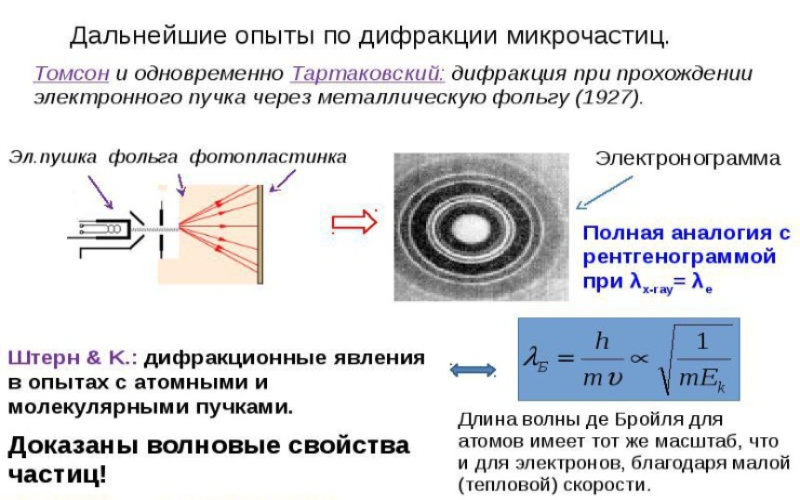
При проведении дифракционных опытов Томсоном, на фотопластинке формировалась система темных концентрических колец. Становится ясно, что вероятность обнаружения и каждого из испущенных электронов окажется неодинаковой в разных местах фотопластинки. Так, в области темных концентрических колец она будет больше, сравнительно с остальными зонами экрана.

Рисунок 3. Опыты по дифракции микрочастиц.

С волновой точки зрения, присутствие максимума количества электронов в определенных направлениях предполагает соответствие данных направлений наибольшей интенсивности волны де Бройля, что послужило в качестве основания для статистического истолкования волны де Бройля.

Специальная теория относительности стала фундаментальной основой по установлению и формированию свойств четвертого измерения. Оно получило название пространства-времени. В это же время начали продвигаться теоретические представления о релятивистской механике. Позже все принципы нового раздела физики получили свои научные подтверждения и до сих пор являются основными принципами изучения физического мира, движения и взаимодействия частиц, представления материи.

Заключение

Конечно можно много говорить по теме Статистический смысл волновой функции, но основную суть мы изложили по этому вопросу. Если вам нужно дополнительная консультация, пожалуйста пишите ваши сообщения нам на почту. Все поступившие вопросы рассматриваются и не остаются без ответа.