Мгновенная скорость и ускорение

По просьбе нашего читателя постараемся описанную тему от 07:37 | 11.04.2016 раскрыть ещё глубже, сегодня рассмотрим Мгновенная скорость и ускорение. Не будем разливать воду, а преступим рассмотрению этого вопроса.

Основное положение

Скорость тела или материальной точки называют мгновенной, если она есть в конкретный момент времени или в заданной точке траектории движения. Это значение называют предельным, поскольку к нему стремится средняя скорость тела при бесконечном уменьшении промежутка времени. Его обозначают $Δt$.

Мгновенная скорость выражается по следующей формуле:

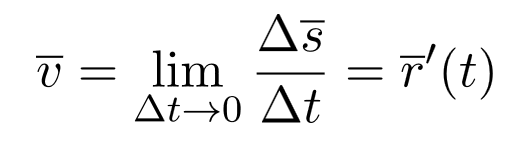
Рисунок 2. Мгновенная скорость.

Величина, которая определяет изменения в наборе скорости тела, называется ускорением. Это предельные значения величины и к ней стремится изменения скорости при бесконечном уменьшении промежутка времени $Δt$.

Перемещение при равномерном прямолинейном движении рассчитывается по формуле:

$Δx = υxt$

Величина $υx$ – проекция скорости на ось Х.

Отсюда следует, что закон равномерного прямолинейного движения имеет следующий вид:

$x = xo + υxt$

В начальный момент времени $xo = 0$, поэтому остальные значения приобретают вид:

$x = υxt$.



Определение 1

При переменном движении скорость тела с течением времени меняется, по этой причине для характеристики подобного перемещения применяются определения средней и моментальной скоростей.

Средней скоростью переменного движения $v_{cp}$ называют векторную величину, равную отношению перемещения тела $s$ к промежутку времени $t$, в течении которого оно совершило перемещение:

$v_{cp} = lim\left(\frac{Ds}{Dt}\right)$.

Переменное перемещение внедряет в процесс только лишь тот интервал времени, для которого эта скорость установлена. Мгновенной скоростью является скорость, какой тело обладает в определенный период времени (и значит, в конкретной точке траектории). Мгновенная скорость $v$ является пределом, к которому устремляется средняя скорость точки $v_{cp}$, в то время как промежуток времени движения точки стремится к 0:

$v = lim\left(\frac{Ds}{Dt}\right)$.

Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к 0 (если этот порог существует), выступает главной производной этой функции по данному аргументу.

Изучим, как скатывается шарик с наклонной плоскости. Шар перемещается неровно: пути, проходимые им за последовательные одинаковые интервалы периода, увеличиваются. Таким образом, темп передвижения шарика возрастает. Перемещение объекта, скатывающегося с косой плоскости, считается классическим примером прямолинейного равноускоренного перемещения.

Рассмотрим определение равноускоренного движения.

Определение 2

Прямо равноускорено способен передвигаться, к примеру, транспорт в период разгона. Но необычным может представиться в таком случае, то что во время торможения машина также способна передвигаться прямолинейно равноускорено! Так как в определении равноускоренного перемещения речь никак не идет не о росте стремительности, а только лишь об изменении скорости.

Суть в том, что представление ускорения в физике обширнее, нежели в обыденном понимании. В повседневной речи под ускорением подразумевают как правило только лишь повышение быстроты. Мы в физике станем говорить, то что тело перемещается с ускорением постоянно, если быстрота тела меняется любым способом (возрастает либо снижается согласно модулю, меняется согласно направленности и т.п.).

Может возникнуть вопрос: по какой причине мы уделяем внимание непосредственно прямолинейному равноускоренному перемещению? Забегая немножко вперед, скажем, что с этим перемещением мы будем часто иметь дело при рассмотрении законов механики.

Напомним, что под воздействием стабильной силы тело перемещается прямо равноускорено. (В случае если первоначальная скорость тела равна нулю либо ориентирована по линии воздействия силы.) А в многочисленных задачах из сферы механики рассматривается непосредственно такая ситуация, в которой применяются уравнения прямолинейного равноускоренного движения, формулы конечной скорости и формулы пути без времени.



Заключение

Конечно можно много говорить по теме Мгновенная скорость и ускорение, но основную суть мы изложили по этому вопросу. Если вам нужно дополнительная консультация, пожалуйста пишите ваши сообщения нам на почту. Все поступившие вопросы рассматриваются и не остаются без ответа.