Квантовая статистика Ферми-Дирака

По просьбе нашего читателя постараемся описанную тему от 01:39 | 04.03.2013 раскрыть ещё глубже, сегодня рассмотрим Квантовая статистика Ферми-Дирака. Не будем разливать воду, а преступим рассмотрению этого вопроса.

Основное положение

В статистической физике статистика Ферми-Дирака представляет квантовую статистику, применяемую в отношении систем тождественных фермионов (зачастую, - , частиц с полуцелым спином, в отношении которых действует принцип запрета Паули). Иными словами, в ее задачи входит определение распределения вероятностей нахождения фермионов на энергетических уровнях системы, пребывающей в термодинамическом равновесии.

Она была предложена в 1926 Э. Ферми и П. Дираком, которому удалось выяснить ее квантово-механический смысл, также она позволяет определить вероятность, с которой фермион займет данный энергетический уровень.

Публикация работ вышеуказанных физиков появилась в 1926 году, а уже в следующем году ее принципы активно применил в своих исследованиях ученый А. Зоммерфельд в отношении электронов в металле.

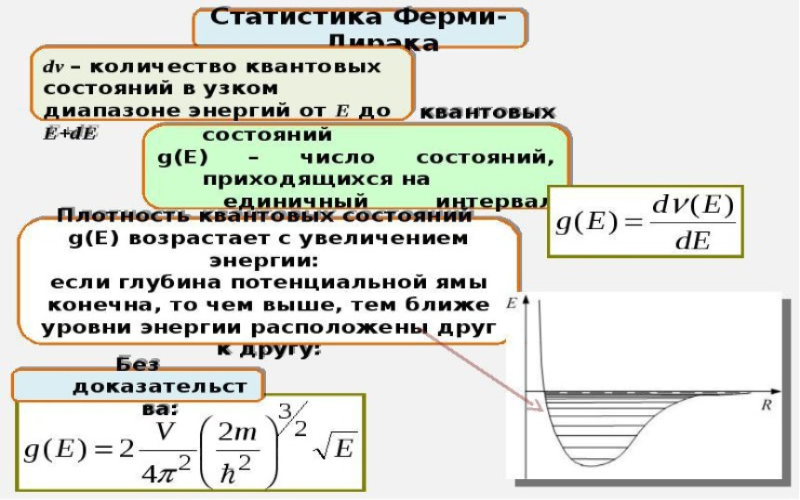
Рисунок 4. Статистика Ферми-Дирака.

Таким образом, статистики Ферми-Дирака и Бозе-Эйнштейна активно используются в случае необходимости учета квантовых эффектов (в ситуации обладания частицами «неразличимостью».

Квантовая концентрация представляет определенную концентрацию, расстояние между частицами при которой оказывается соразмерным длине волны де Бройля. То есть, это происходит в ситуации, когда волновые функции частиц будут соприкасаемыми, однако при этом они не перекрываются.

Квантовая концентрация зависима от температуры. Разделяют следующие принципы вышеуказанных статистик:

• статистика Ферми-Дирака применима в отношении фермионов (частиц, на которые оказывает непосредственное воздействие принцип Паули);
• статистика Бозе-Эйнштейна применима к бозонам.

Оба данных распределения при высоких температурах становятся распределением Максвелла-Больцмана.

Определение 1

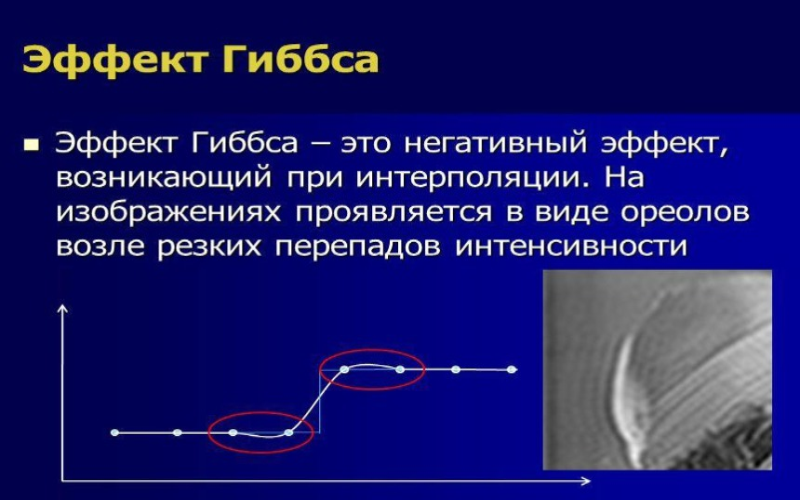
Рисунок 1. Эффект Гиббса.

Изучаемые системы могут быть как классическими, так и квантовыми. Современная статистическая физика, основанная на методе Гиббса, подразделяется на:

• классическую статистику;
• квантовую статистику (считается более общей и строгой, поскольку из нее возможно получение всех базовых положений классической статистической физики).

Подобное деление относится непосредственно к выделению в классическую статистику определенных вопросов, решение которых исключает необходимость квантовых представлений.

Зачастую статистическую физику называют еще статистической механикой, однако подобному названию присущ исключительно исторический смысл, и связано оно с приложением статистики к аналитической механике.

Также в формате рассмотрения термодинамических вопросов, из общей статистической физики выделяется такой раздел, как статистическая термодинамика, представляющая наиболее развитую часть статистики в наиболее полном масштабе.

Заключение

Конечно можно много говорить по теме Квантовая статистика Ферми-Дирака, но основную суть мы изложили по этому вопросу. Если вам нужно дополнительная консультация, пожалуйста пишите ваши сообщения нам на почту. Все поступившие вопросы рассматриваются и не остаются без ответа.